Logarithms
Logarithms are used to simplify math. Multiplication and division can be accomplished through addition and subtraction.
log(1) = 0
log(number greater than 1) = positive
log(number less than 1) = negative
log(A•B) = log(A) + log(B)
log(A/B) = log(A) - log(B)
log(A)n = n•log(A)
Power
ratio expressed in dB
dB stands for decibel (1/10 of a Bel). The dB is a way of expressing the ratio between two power levels logarithmically.
![]()
P(dB) = Numerical power ratio expressed in dB
P1 = Power 1 (input)
P2 = Power 2 (output)
Decibels can be added and subtracted to determine the total gain of a system.

Pout = 10dBm + 5dB - 10dB + 20dB = 25dBm
|
P(dB) = 10 log10 (P2/P1) |
Ratio |
V(dB) = 20 log10 (V2/V1) |
|
120 |
1.00E+12 |
240 |
|
90 |
1.00E+09 |
180 |
|
60 |
1.00E+06 |
120 |
|
50 |
1.00E+05 |
100 |
|
40 |
1.00E+04 |
80 |
|
30 |
1000 |
60 |
|
20 |
100 |
40 |
|
10 |
10 |
20 |
|
9.5 |
9 |
19.1 |
|
9.0 |
8 |
18.1 |
|
8.5 |
7 |
16.9 |
|
7.8 |
6 |
15.6 |
|
7.0 |
5 |
14.0 |
|
6.0 |
4 |
12.0 |
|
4.8 |
3 |
9.5 |
|
3.0 |
2 |
6.0 |
|
0 |
1 |
0 |
|
-0.5 |
0.9 |
-0.9 |
|
-1.0 |
0.8 |
-1.9 |
|
-1.5 |
0.7 |
-3.1 |
|
-2.2 |
0.6 |
-4.4 |
|
-3.0 |
0.5 |
-6.0 |
|
-4.0 |
0.4 |
-8.0 |
|
-5.2 |
0.3 |
-10.5 |
|
-7.0 |
0.2 |
-14.0 |
|
-10 |
0.1 |
-20 |
|
-20 |
0.01 |
-40 |
|
-30 |
0.001 |
-60 |
|
-40 |
1.00E-04 |
-80 |
|
-50 |
1.00E-05 |
-100 |
|
-60 |
1.00E-06 |
-120 |
|
-90 |
1.00E-09 |
-180 |
|
-120 |
1.00E-12 |
-240 |
Power
expressed in dBm
Most of the time, power is expressed in dBm in RF applications. dBm is power relative to one milliwatt.
![]()
Voltage
ratio expressed in dB
As long as you use a consistent resistance you can express voltage as a logarithmic ratio as follows:
![]()
![]() and
and ![]()
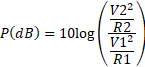
![]()
![]()
![]()
When R1 = R2 the second term goes to 0.
![]()
V(dB) = Numerical voltage ratio expressed in dB
V1 = Voltage 1 (input)
V2 = Voltage 2 (output)
end